Learning Unsupervised Hierarchical Part Decomposition
of 3D Objects from a Single RGB Image

Despoina Paschalidou 1,3,5 Luc van Gool 3,4,5 Andreas Geiger 1,2,5
1 Autonomous Vision Group, MPI for Intelligent Systems Tübingen 2 University of Tübingen
3 Computer Vision Lab, ETH Zürich 4 KU Leuven
5 Max Planck ETH Center for Learning Systems
CVPR 2020

Paper
Code
Video
Poster
Slides
Blog
We consider the problem of learning structure-aware representations that go beyond part-level geometry and focus on part-level relationships. Here, we show our reconstruction as an unbalanced binary tree of primitives, given a single RGB image as input. Note that our model does not require any supervision on object parts or the hierarchical structure of the 3D object. We show that our representation is able to model different parts of an object with different levels of abstraction, leading to improved reconstruction quality.
Humans perceive the 3D world as a set of distinct objects that are characterized by various low-level (geometry, reflectance) and high-level (connectivity, adjacency, symmetry) properties. Recent methods based on convolutional neural networks (CNNs) demonstrated impressive progress in 3D reconstruction, even when using a single 2D image as input. However, the majority of these methods focuses on recovering the local 3D geometry of an object without considering its part-based decomposition or relations between parts. We address this challenging problem by proposing a novel formulation that allows to jointly recover the geometry of a 3D object as a set of primitives as well as their latent hierarchical structure without part-level supervision. Our model recovers the higher level structural decomposition of various objects in the form of a binary tree of primitives, where simple parts are represented with fewer primitives and more complex parts are modeled with more components. Our experiments on the ShapeNet and D-FAUST datasets demonstrate that considering the organization of parts indeed facilitates reasoning about 3D geometry.
Approach Overview
Our structure-aware representation is based on the simple assumption that complex object parts should be modelled with more primitives, whereas geometrically simpler parts with fewer components. In contrast to existing primitive-based techniques that represent 3D objects as an unstructured collection of parts, we employ a neural network that learns to recursively decompose an object into its constituent parts by building a latent space that encodes both the part-level hierarchy and the part geometries. The hierarchical decomposition is represented as an unbalanced binary tree of primitives of depth \(D\).
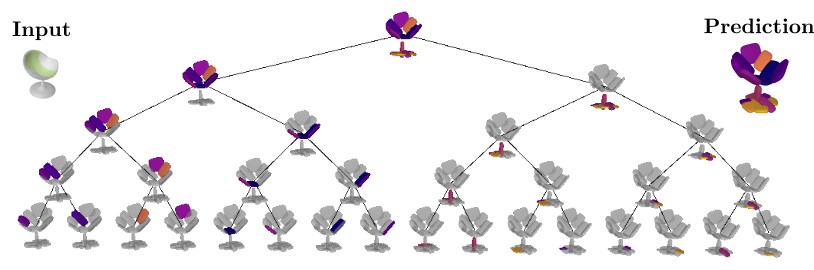
At every depth level, each of the \(2^d \mid d=0,\dots, D\) nodes is recursively split into two nodes (its children) until reaching the maximum depth. This results in a representation with various levels of detail. Naturally, reconstructions from deeper depth levels are more detailed. Note that the reconstructions below are derived from the same model, trained with a maximum number of \(2^4=16\) primitives. During inference, the network dynamically combines representations from different depth levels to recover the final prediction.

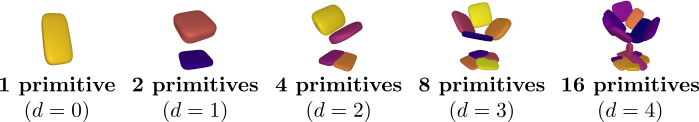
More importantly, the hierarchical part-based decomposition is learned without any supervision neither on the object parts nor their structure. Instead, our model jointly infers these latent variables during training.

Given an input (e.g. image, voxel grid), our goal is to learn a neural network \(\phi_{\theta}\) which maps the input to a set of primitives that best describe the target object. We represent the target object as a set of points \(\mathcal{X}=\{(\mathbf{x}_i, o_i)\}_{i=1}^N\) where \(mathbf{x}_i\) corresponds to the location of the \(i\)-th point and \(o_i\) denotes its label, namely whether this point lies inside or outside the target object. During training, our network learns to predict a hierarchical decomposition over parts in the form of a binary tree of primitives of depth \(D\) as $$\mathcal{P}=\{\{p_k^d\}_{k=0}^{2^d-1} \,\mid \, d=\{0 \dots D\}\}.$$ Our network comprises three main components:
Given an input (e.g. image, voxel grid), our network predicts a binary tree of primitives \(\mathcal{P}\) of maximum depth \(D\). The feature encoder maps the input into a feature vector \(\mathbf{c}_0^0\). Subsequently, the partition network splits each feature representation \(\mathbf{c}_k^d\) in two \(\{\mathbf{c}_{2k}^{d+1}, \mathbf{c}_{2k+1}^{d+1}\}\), resulting in feature representations for \(\{1,2,4,\dots, 2^d\}\) primitives where \(\mathbf{c}_k^d\) denotes the feature representation for the \(k\)-th primitive at depth \(d\). Each \(\mathbf{c}_k^d\) is passed to the structure network that "assigns" a part of the object to a specific primitive \(p_k^d\). As a result, each \(p_k^d\) is responsible for representing a specific part of the target shape, denoted as the set of points \(\mathcal{X}_k^d\). Finally, the geometry network predicts the primitive parameters \(\lambda_k^d\) and the reconstruction quality \(q_k^d\) for each primitive. We use plate notation to denote repetition over all nodes \(k\) at each depth level \(d\). The final reconstruction is shown on the right. Our optimization objective is a weighted sum over four terms:
Evaluation on ShapeNet
We evaluate our model on the single-view 3D reconstruction task and compare against various state-of-the-art methods. We follow the standard experimental setup and train a single model for the 13 ShapeNet objects.
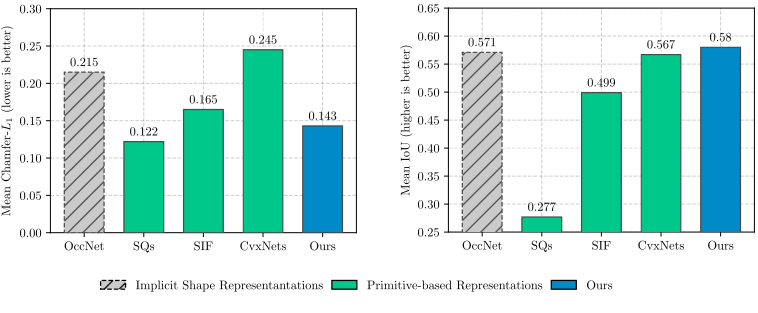
Our model yields geometrically accurate reconstructions that outperform existing primitive-based methods, while performing competitively with more flexible implicit share representations, such as Occupancy Networks.
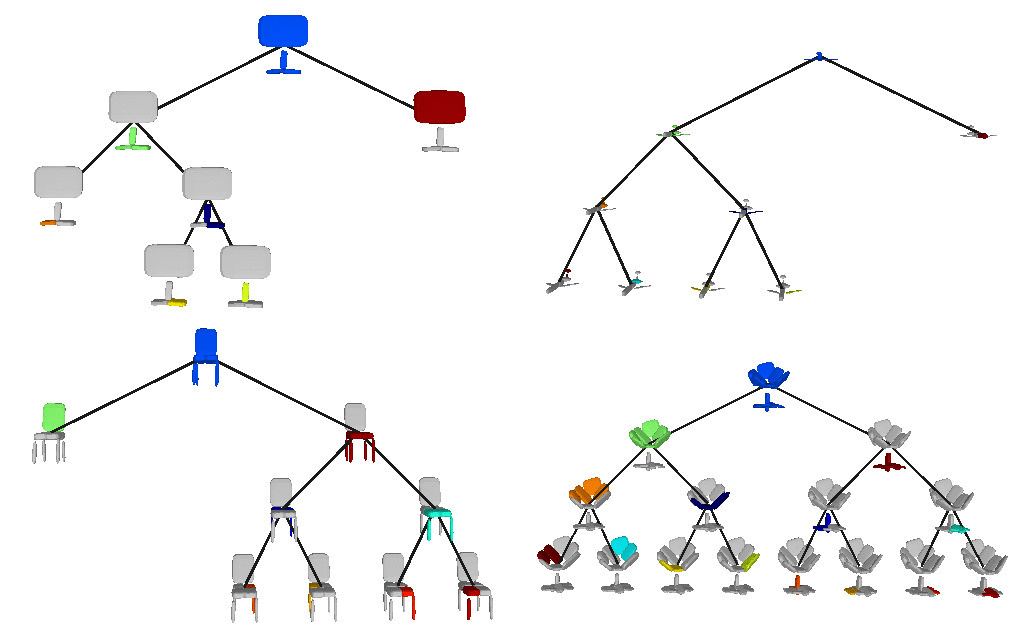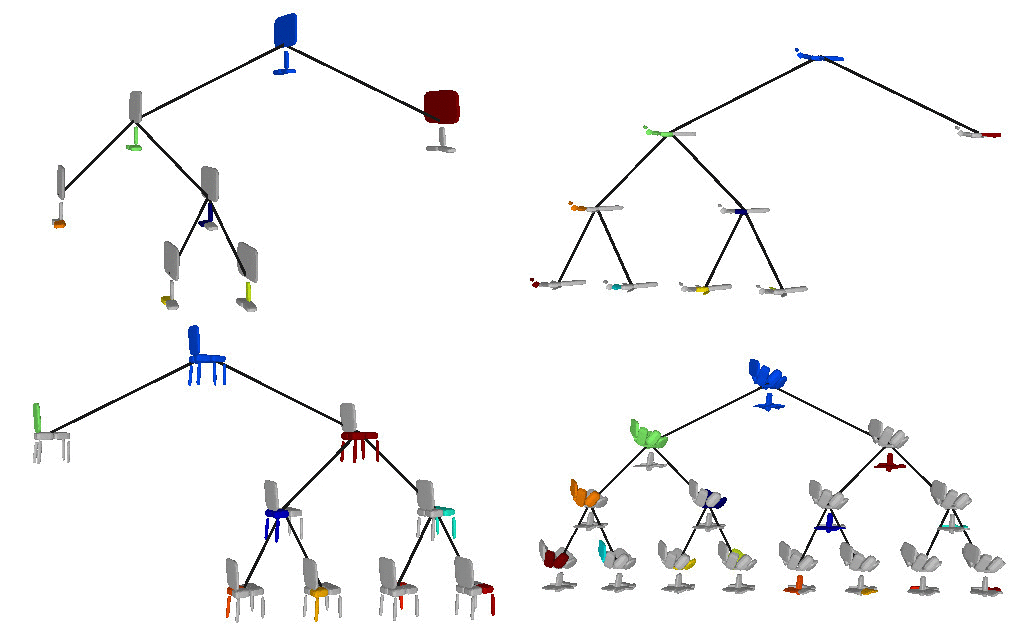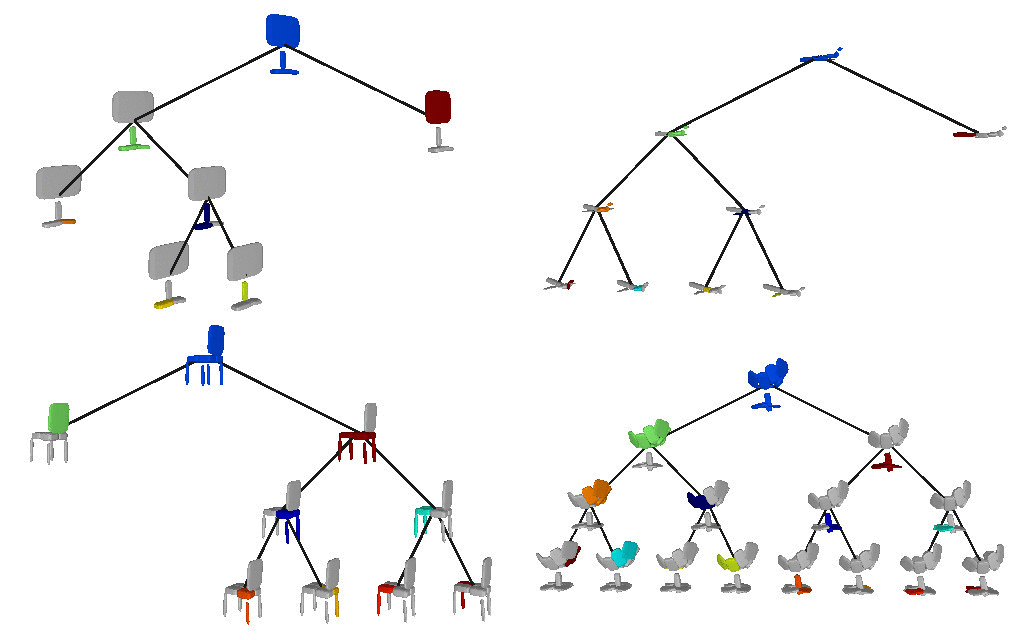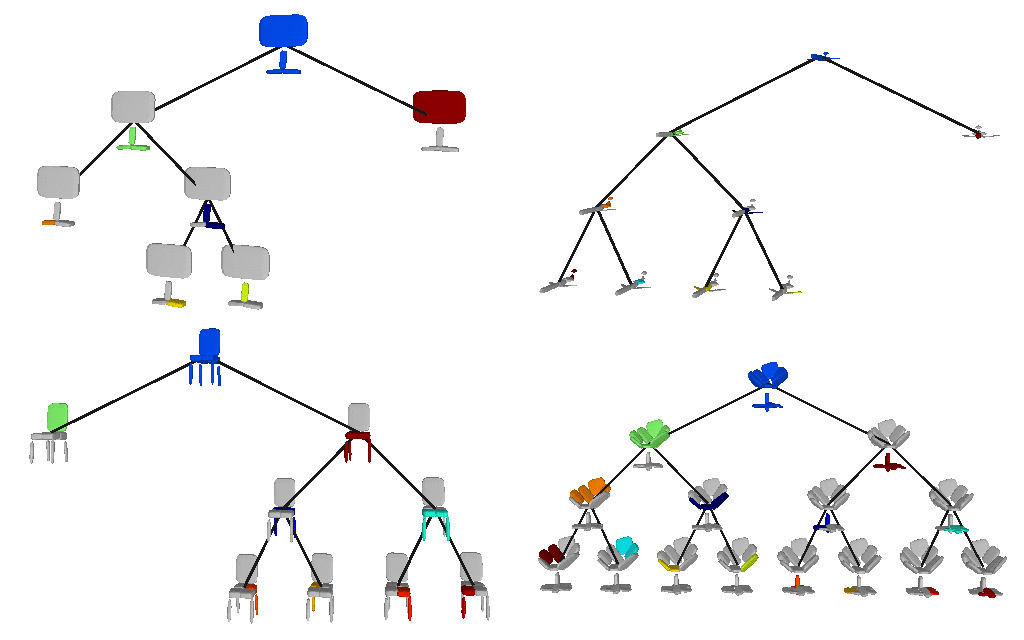
Below we visualize the predicted tree of primitives on various ShapeNet objects. We observe that our model recovers unbalanced binary trees of primitives that decompose a 3D object into a set of parts. We associate every primitive with a unique color, thus primitives illustrated with the same color correspond to the same object part. Note how our model uses fewer primitives for representing simpler parts (e.g. screen of the monitor) and more primitives for more complex parts (e.g. wings of the plane).
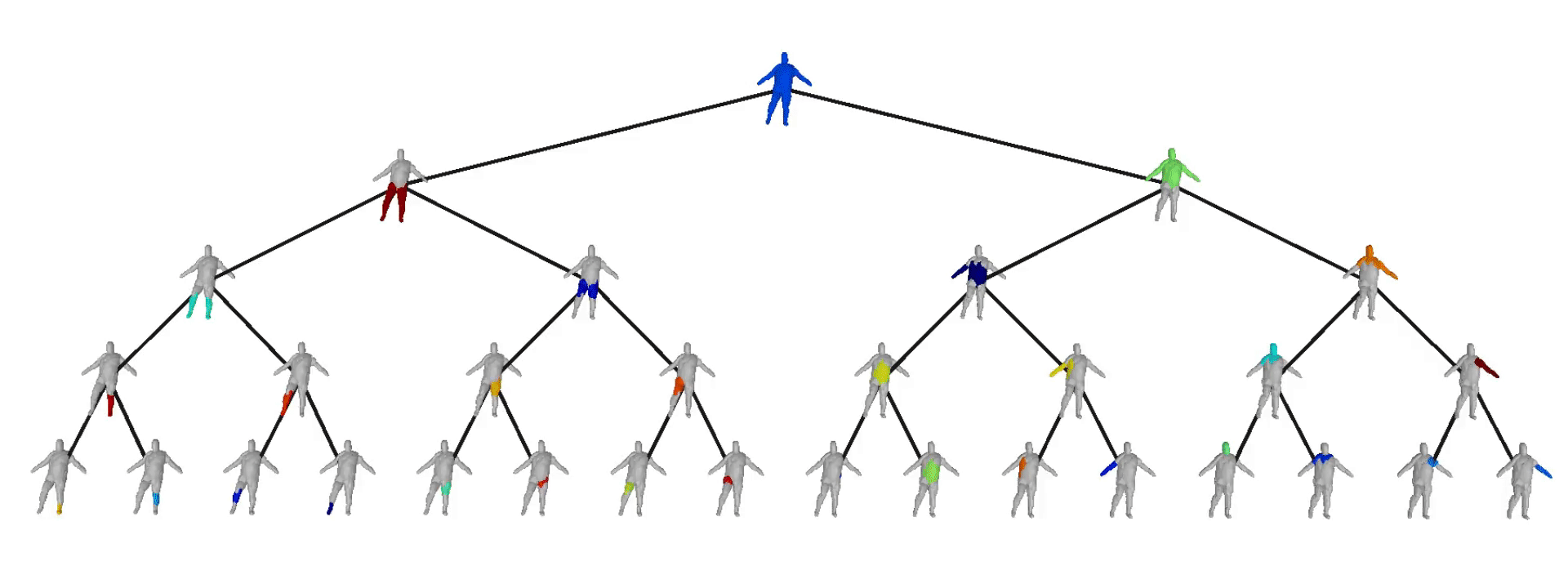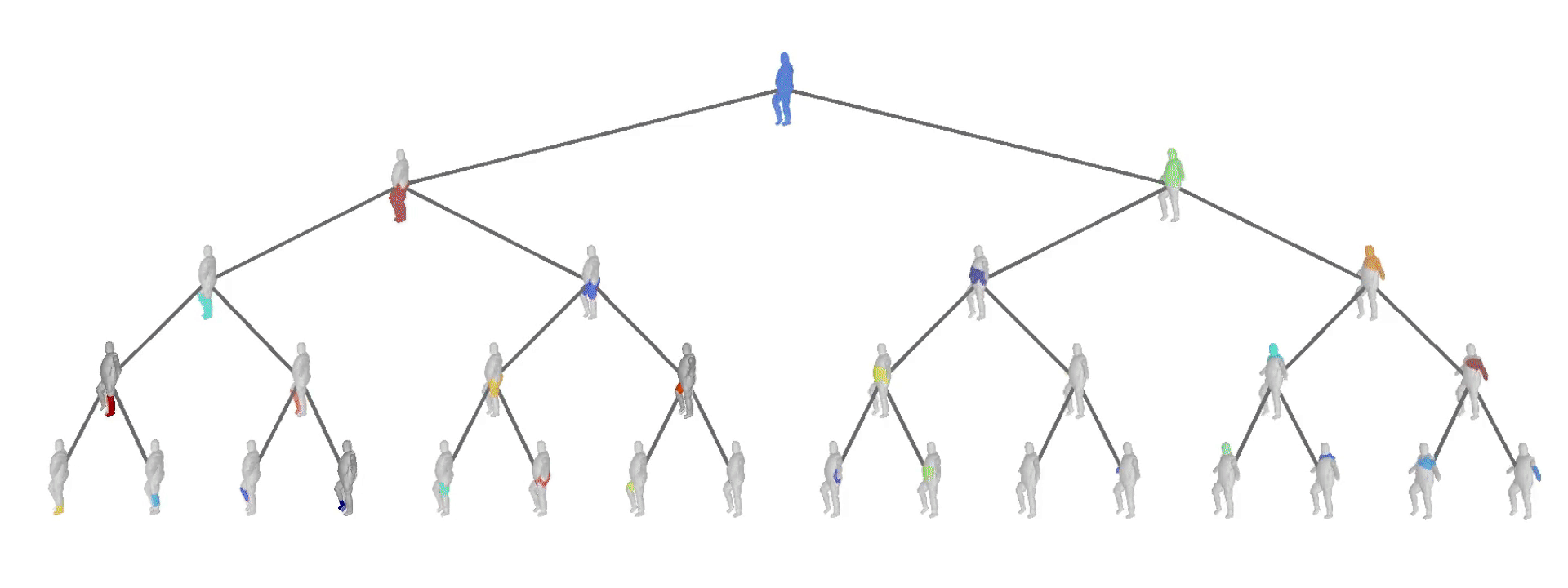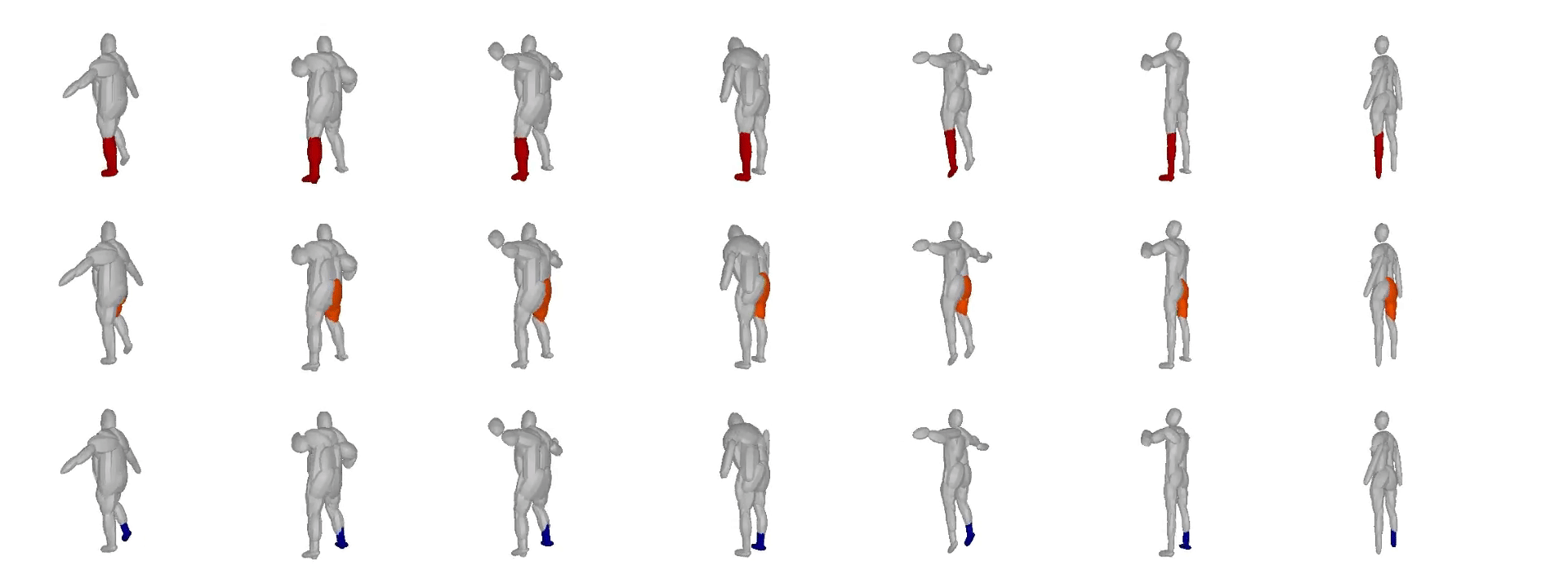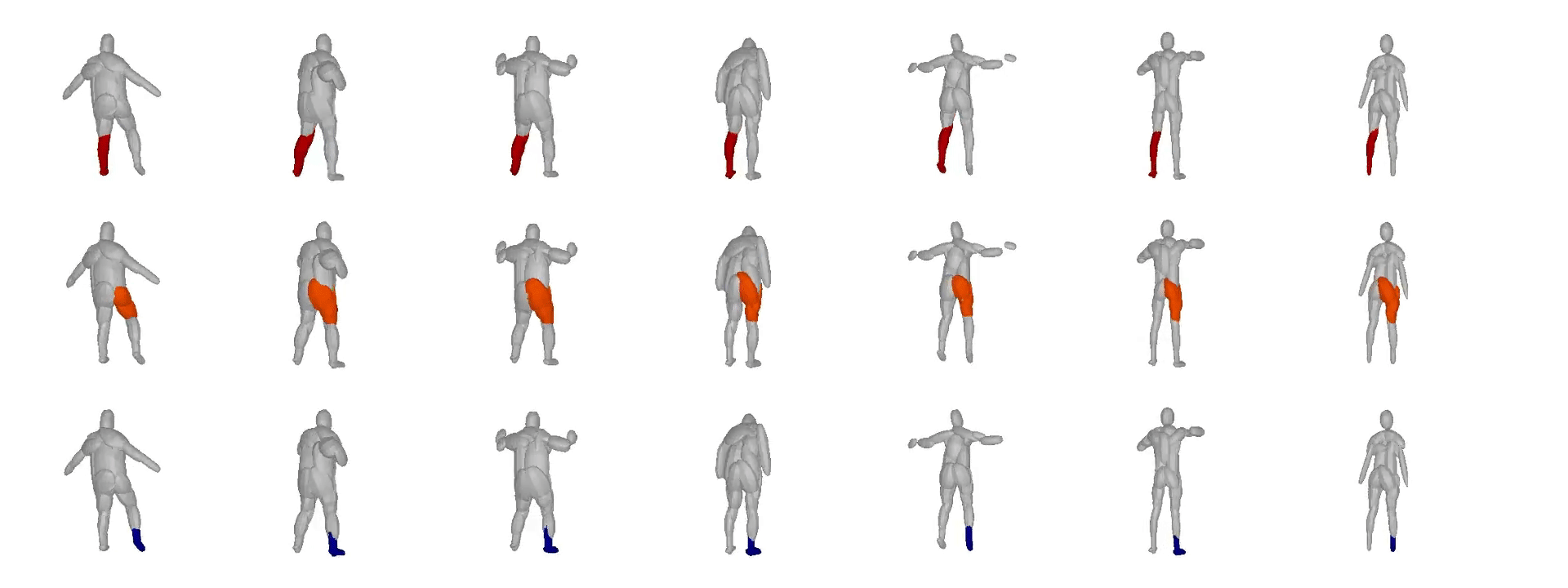
Evaluation on Dynamic FAUST
We also evaluate our model on the Dynamic FAUST dataset, which consists of various humans under different poses. We observe that while our baseline yields more parsimonious abstractions, their level of detail is limited. On the contrary, our model captures the geometry of the human body with more detail.
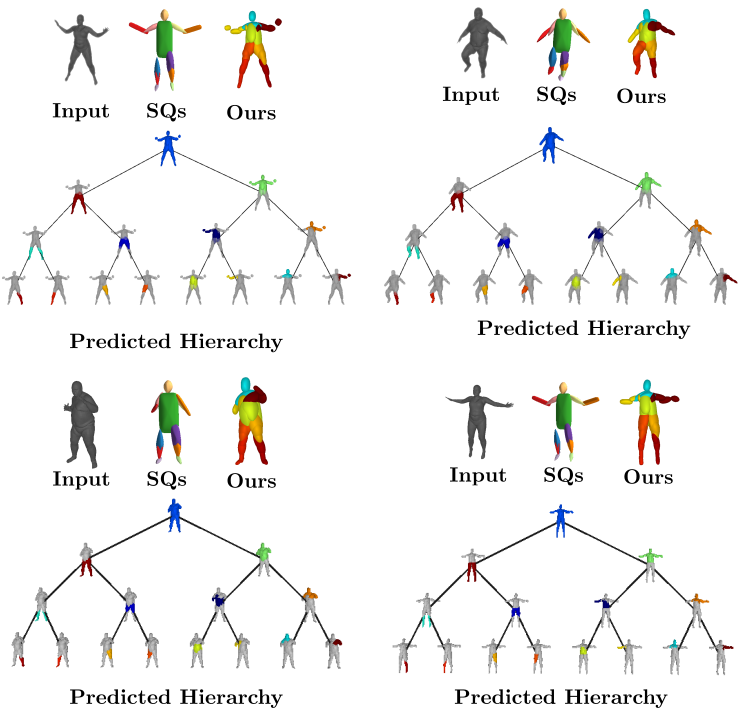
We further observe that our learned hierarchies have a semantic interpretation, as the same node is consistently used for representing the same object part. For example, the node (4, 3) is consistently used for representing the right leg of different humans under various poses (illustrated with blue), while node (4, 12) is used for representing the head of different humans (illustrated with light green).
Acknowledgements
This research was supported by the Max Planck ETH Center for Learning Systems and a HUAWEI research gift.